Acceleration, velocity, position problems--
A couple of problems this week are acceleration/velocity/position problems.
To do these problems, you need to remember that the derivative of position is velocity (i.e., velocity is the rate of change of position) and the derivative of velocity is acceleration (i.e., acceleration is the rate of change of velocity).
In these problems, we use the definitions in the previous paragraph in reverse: because the derivative of position is velocity, then we know that the integral of velocity is position (or displacement -- it tells how far and which way the object moves from where it started).
Example 1: Suppose that you know the velocity of an object at time t seconds is ![]() feet per second. And you know that at time t = 0, the position of the particle is x = 5. What is the position of the particle 4 seconds later?
feet per second. And you know that at time t = 0, the position of the particle is x = 5. What is the position of the particle 4 seconds later?
Solution: The problem tells us that ![]() and that x(0) = 5. To find the function x(t), we need to integrate its (known) derivative:
and that x(0) = 5. To find the function x(t), we need to integrate its (known) derivative:
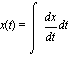 =
= 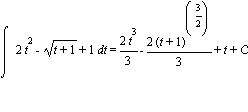
(To do the integral of ![]() , you can use the substitution u = t + 1.)
, you can use the substitution u = t + 1.)
To find the value of the constant C, use the fact that x(0) = 5. Putting x = 5 on the left side of the equation and t = 0, you can see that 5 = 0 - 2/3 + 0 + C, so C = 17/3. Therefore,
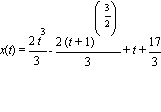 .
.
The problem asked for the position 4 seconds later, in other words, for the value of x(4). So we substitute t = 4 into the expression for x(t):
![]() =
= ![]() feet (after some simplification and rationalization of the denominator).
feet (after some simplification and rationalization of the denominator).
Example 2: Suppose you know that the acceleration of a particle is 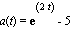 meters per second squared, and you know that the particle "starts from rest" (i.e., its initial velocity v(0) is equal to zero). How far is the particle from its starting point, and which way is it moving 2 seconds later?
meters per second squared, and you know that the particle "starts from rest" (i.e., its initial velocity v(0) is equal to zero). How far is the particle from its starting point, and which way is it moving 2 seconds later?
Solution: Since we're given the acceleration here, we have to integrate to find the velocity, and then integrate again to find the displacement (position). First, velocity:
![]() =
= 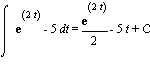
(the substitution u = 2t might help with the integral of the exponential.)
To find C, we use the fact that v(0) = 0. This gives the equation 0 = 1/2 - 0 + C (since ![]() ), so we get that C =
), so we get that C = ![]() . We now know that
. We now know that
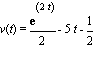 .
.
The question asks how far away (displacement) of the object from its starting point 2 seconds later. This means it wants to know what is x(2) - x(0) . But the fundamental theorem of calculus tells us that
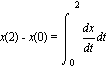 .
.
And since dx/dt = v(t), we see that this displacement is
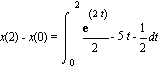 =
= 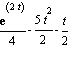 (evaluated at 2 and 0)
(evaluated at 2 and 0)
So x(2) - x(0) = 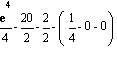 =
= ![]() = about 2.4 meters
= about 2.4 meters
So x is 4.4 meters in the positive direction from where it started.
Which way is it moving? This depends on the sign (+ or -) of v(2). So we evaluate:
v(2) = ![]() = about 16.8 meters per second -- in the positive direction.
= about 16.8 meters per second -- in the positive direction.
So the velocity is in the same direction as the displacement, and the particle is moving away from where it started out.