I'm interested in refining and applying local-to-global methods from algebraic topology to problems in optimization and data analysis. To that end, I am interested in algebraic invariants on topological structures naturally occurring in the real-world but are not amenable to standard homological algebra.

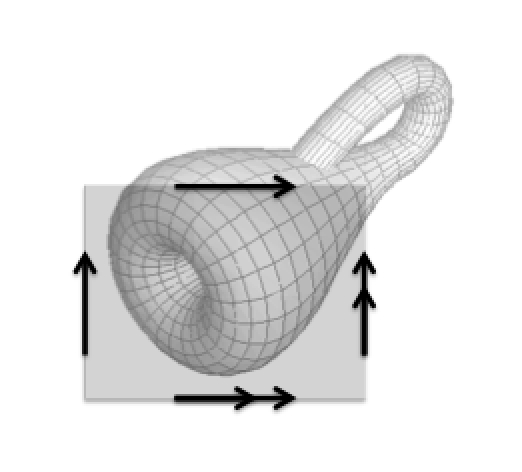Directed Topology Spaces often come equipped with directionality, like vector fields, partial orders, and simplicial orientations. Directed algebraic topology studies algebraic invariants on such spaces that can capture information about the topology and directionality. Directed (co)homology refines classical (co)homology to detect directed structure on a directed space. Examples of directed homology and cohomology respectively include the flows and Poincare sections of dynamical systems. Recent interests of mine include showing how such theories exhibit Alexander and Poincare Dualities. Together with Eric Goubault and Emmanuel Haucourt, I've used directed homology in the past to study the local order structure of locally preordered spaces that arise in computer science [3]. Directed homotopy theory studies directed spaces up to deformations respecting directionality. I'm currently interested in unifying certain aspects of higher category theory and dynamics as a formal equivalence between combinatorial and topological directed homotopy theories, extending previous results on simplicial and cubical approximation [6]. I've also worked in the past on formally connecting the theory of computation with directed homotopy [2] and developing adequate categorical foundations [1].

Applied Topology Data analysis, which often takes the form of global geometric inferences from sample points whose local metric structure only is known, naturally lends itself to sheaf-theoretic methods. Together with Rob Ghrist, Dave Lipsky, Michael Robinson, Hank Owen, and Mike Stein, I'm working on software that analyzes video imagery by means of homological invariants on sheaves. Optimization dualities sometimes make seemingly intractable computations simple and fast. Recently, I've been working on interpreting and generalizing flow-cut dualities as special cases of a Poincare Duality for sheaves on directed graphs [8]. Together with Rob Ghrist and Greg Henselman, I'm interested in applying such a generalized flow-cut duality to handle logical, stochastic, and multicommodity constraints on directed graphs [7] and higher dimensional spaces. Semantics and Homotopy The use of directed spaces to model computation dates back to early work on the Lambda Calculus. Recently, I've become interested in directed extensions of homotopy type theory. Together with Eric Goubault and Emmanuel Haucourt, I've worked in the past on using directed homotopy theory to automate the formal verification of large, concurrent programs [4].