Simulation solutions of the Stochastic Differential Equation
dW = 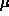 dt +
dt +  dX
dX
dW = 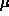 dt +
dt +  dX
dX
This is the simplest stochastic differential equation -- its solution is a
Wiener process (Brownian motion) with drift coefficient
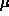 and diffusion coefficient
and diffusion coefficient  .
.
By the analysis in the preceding lecture notes, we know to expect the solution
W(t) to be a random variable, normally distributed with mean
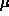 t and standard deviation
t and standard deviation  sqrt(t).
sqrt(t).
In this simulation, you get to use the slider bars to set
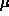 and
and  , and then
have the simulation repeatedly construct a (Brownian) path with the
parameters you have chosen. You can compare the
stochastic simulation (blue graph) with the solution of the
deterministic differential equation dW=
, and then
have the simulation repeatedly construct a (Brownian) path with the
parameters you have chosen. You can compare the
stochastic simulation (blue graph) with the solution of the
deterministic differential equation dW=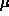 dt
(pink graph). At the right of the graph, the number of times
the path ends in each of the intervals delineated by the black lines is
tallied (after you set
dt
(pink graph). At the right of the graph, the number of times
the path ends in each of the intervals delineated by the black lines is
tallied (after you set 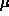 and
and  , you can choose how many intervals you would like
to consider).
, you can choose how many intervals you would like
to consider).
After you have done a number of simulations (you may need to do at least one or two hundred to get good statistics) you can see the results of the simulation (for t=10) summarized against the theoretical probability distribution. In order to help you complete a large number of simulations quickly, you may click on the "many" button to do them 25 at a time.
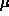 and
and  .
.