![]()
| Nature 427, 244 - 247 (15 January 2004); doi:10.1038/nature02169 |
|
KONRAD P. KÖRDING AND DANIEL M. WOLPERT
When we
learn a new motor skill, such as playing an approaching tennis ball,
both our sensors and the task possess variability. Our sensors provide
imperfect information about the ball's velocity, so we can only
estimate it. Combining information from multiple modalities can reduce
the error in this estimate1-4. On a longer
time scale, not all velocities are a priori equally probable, and over
the course of a match there will be a probability distribution of
velocities. According to bayesian theory5, 6,
an optimal estimate results from combining information about the
distribution of velocities—the prior—with evidence from sensory
feedback. As uncertainty increases, when playing in fog or at dusk, the
system should increasingly rely on prior knowledge. To use a bayesian
strategy, the brain would need to represent the prior distribution and
the level of uncertainty in the sensory feedback. Here we control the
statistical variations of a new sensorimotor task and manipulate the
uncertainty of the sensory feedback. We show that subjects internally
represent both the statistical distribution of the task and their
sensory uncertainty, combining them in a manner consistent with a
performance-optimizing bayesian process4, 5. The central nervous system therefore employs probabilistic models during sensorimotor learning.
Subjects
reached to a visual target with their right index finger in a
virtual-reality set-up that allowed us to displace the visual feedback
of their finger laterally relative to its actual location (Fig. 1a;
see Methods for details). On each movement, the lateral shift was
randomly drawn from a prior distribution that was gaussian with a mean
shift of 1 cm to the right and a standard deviation of 0.5 cm
(Fig. 1b).
We refer to this distribution as the true prior. During the movement,
visual feedback of the finger position was only provided briefly,
midway through the movement. We manipulated the reliability of this
visual feedback on each trial. This feedback was either provided
clearly ( 0 condition, in which the uncertainty comes from intrinsic processes only), blurred to increase the uncertainty by a medium (
0 condition, in which the uncertainty comes from intrinsic processes only), blurred to increase the uncertainty by a medium ( M) or large (
M) or large ( L) amount, or was withheld altogether leading to infinite uncertainty (
L) amount, or was withheld altogether leading to infinite uncertainty (
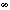 ). Visual information about the position of the finger at the end of the movement was provided only on clear feedback trials (
). Visual information about the position of the finger at the end of the movement was provided only on clear feedback trials ( 0) and subjects were instructed to get as close to the target as possible on all trials.
0) and subjects were instructed to get as close to the target as possible on all trials.
 |
Figure 1
The experiment and models.
Full legend High resolution image and legend (70k) |
Subjects were
trained for 1,000 trials on the task, to ensure that they experienced
many samples of the lateral shift drawn from the underlying gaussian
distribution. After this period, when feedback was withheld (
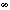 ), subjects pointed 0.97
), subjects pointed 0.97 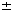 0.06 cm (mean
0.06 cm (mean 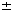 s.e.m. across subjects) to the left of the target showing that they had
learned the average shift of 1 cm experienced over the ensemble of
trials (Fig. 1a,
example finger and cursor paths shown in green). Subsequently, we
examined the relationship between imposed lateral shift and the final
location that subjects pointed to. On trials in which feedback was
provided, there was compensation during the second half of the movement
(Fig. 1a,
example finger and cursor paths for a trial with lateral shift of
2 cm shown in blue). The visual feedback midway through the
movement provides information about the current lateral shift. However,
we expect some uncertainty in the visual estimate of this lateral
shift. For example, if the lateral shift is 2 cm, the distribution
of sensed shifts over a large number of trials would be expected to
have a gaussian distribution centred on 2 cm with a standard
deviation that increases with the blur (Fig. 1c).
s.e.m. across subjects) to the left of the target showing that they had
learned the average shift of 1 cm experienced over the ensemble of
trials (Fig. 1a,
example finger and cursor paths shown in green). Subsequently, we
examined the relationship between imposed lateral shift and the final
location that subjects pointed to. On trials in which feedback was
provided, there was compensation during the second half of the movement
(Fig. 1a,
example finger and cursor paths for a trial with lateral shift of
2 cm shown in blue). The visual feedback midway through the
movement provides information about the current lateral shift. However,
we expect some uncertainty in the visual estimate of this lateral
shift. For example, if the lateral shift is 2 cm, the distribution
of sensed shifts over a large number of trials would be expected to
have a gaussian distribution centred on 2 cm with a standard
deviation that increases with the blur (Fig. 1c).
There are
several possible computational models that subjects could use to
determine the compensation needed to reach the target on the basis of
the sensed location of the finger midway through the movement. First
(model 1), subjects could compensate fully for the visual estimate of
the lateral shift. In this model, increasing the uncertainty of the
feedback for a particular lateral shift (by increasing the blur) would
affect the variability of the pointing but not the average location.
Crucially, this model does not require subjects to estimate their
visual uncertainty or the prior distribution of shifts. Second (model
2), subjects could optimally use information about the prior
distribution and the uncertainty of the visual feedback to estimate the
lateral shift. We can see intuitively why model 1 is sub-optimal. If,
on a given trial, the subject sensed a lateral shift of 2 cm,
there are many true lateral shifts that can give rise to such a
perception. For example, the true lateral shift could be 1.8 cm
with a visual error of +0.2 cm, or it could be a lateral shift of
2.2 cm with a visual error of -0.2 cm. Which of the two
possibilities is more probable? Given gaussian noise on the visual
feedback, visual errors of +0.2 cm and -0.2 cm are equally
probable. However, a true lateral shift of 1.8 cm is more probable
than a shift of 2.2 cm given that the prior distribution has a
mean of 1 cm (Fig. 1b).
If we consider all possible shifts and visual errors that can give rise
to a sensed shift of 2 cm, we find that the most probable true
shift is less than 2 cm. The amount by which it is less depends on
two factors, the prior distribution and the degree of uncertainty in
the visual feedback. As we increase the blur, and thus the degree of
uncertainty, the estimate moves away from the visually sensed shift
towards the mean of the prior distribution (Fig. 1d). Without any feedback (
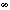 )
the estimate should be the mean of the prior. Such a strategy can be
derived from bayesian statistics and minimizes the subject's mean
squared error.
)
the estimate should be the mean of the prior. Such a strategy can be
derived from bayesian statistics and minimizes the subject's mean
squared error.
A third
computational strategy (model 3) is to learn a mapping from the visual
feedback to an estimate of the lateral shift. By minimizing the error
over repeated trials, subjects could achieve a combination similar to
model 2 but without any explicit representation of the prior
distribution or visual uncertainty. However, to learn such a mapping
requires knowledge of the error at the end of the movement. In our
experiment we only revealed the shifted position of the finger at the
end of the movement on the clear feedback trials ( 0). Therefore, if subjects learn a mapping, they can
only do so for these trials and apply the same mapping to the blurred
conditions (
0). Therefore, if subjects learn a mapping, they can
only do so for these trials and apply the same mapping to the blurred
conditions ( M,
M,  L). This model therefore predicts that the average shift
of the response towards the mean of the prior should be the same for
all amounts of blur.
L). This model therefore predicts that the average shift
of the response towards the mean of the prior should be the same for
all amounts of blur.
By examining the
influence of the visual feedback on the final deviation from the target
we can distinguish between these three models (Fig. 1e).
If subjects compensate fully for the visual feedback (model 1), the
average lateral deviation of the cursor from the target should be zero
for all conditions. If subjects combine the prior and the evidence
provided by sensory feedback (model 2), the estimated lateral shift
should move towards the mean of the prior by an amount that depends on
the sensory uncertainty. For a gaussian distribution of sensory
uncertainty, this predicts a linear relationship between lateral
deviation and the true lateral shift, which should intercept the
abscissa at the mean of the prior (1 cm) and with a slope that
increases with uncertainty. Finally, the mapping model (model 3)
predicts that subjects should compensate for the seen position
independently of the degree of uncertainty. Thus, all conditions should
exhibit the same slope as the clear feedback condition ( 0) of model 2. An examination of the theoretically
determined mean squared error for the three models shows that it is
minimal for model 2. Even though model 1 is on average on target, the
variability in the response is higher than in model 2 (green shading in
Fig. 1e shows the variability for the
0) of model 2. An examination of the theoretically
determined mean squared error for the three models shows that it is
minimal for model 2. Even though model 1 is on average on target, the
variability in the response is higher than in model 2 (green shading in
Fig. 1e shows the variability for the  L condition), leading to a larger mean squared error.
L condition), leading to a larger mean squared error.
The lateral deviation from the target as a function of the lateral shift is shown for a representative subject in Fig. 2a. This shows a slope that increases with increasing uncertainty and is, therefore, incompatible with models 1 and 3. As predicted by model 2, the influence of the feedback on the final pointing location decreases with increasing uncertainty. The slope increases significantly with uncertainty in the visual feedback over the subjects tested (Fig. 2b). The bias and the slope should have a fixed relationship if we assume that subjects do bayesian estimation. We expect no deviation from the target if the true lateral shift is at the mean of the prior (1 cm). This predicts that the sum of the slope and offset should be zero, as observed in Fig. 2c. Subjects thus combine prior knowledge of the distribution with sensory evidence to generate appropriate compensatory movements.
 |
Figure 2
Results for a gaussian distribution.
Full legend High resolution image and legend (57k) |
Assuming that
subjects use a bayesian strategy, we can furthermore use the errors
that the subjects made during the trials to infer their degree of
uncertainty in the feedback. For the three levels of imposed
uncertainty,  0,
0,  M and
M and  L, we find that subjects' estimates of their visual uncertainty are 0.36
L, we find that subjects' estimates of their visual uncertainty are 0.36 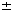 0.04, 0.67
0.04, 0.67 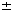 0.1 and 0.8
0.1 and 0.8 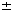 0.1 cm (means
0.1 cm (means 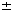 s.e.m. across subjects), respectively. We have also developed a novel
technique that uses these estimates to infer the priors used by the
subjects. Figure 2d
shows the priors inferred for each subject and condition. This shows
that the true prior (red line) was reliably learned by each subject.
s.e.m. across subjects), respectively. We have also developed a novel
technique that uses these estimates to infer the priors used by the
subjects. Figure 2d
shows the priors inferred for each subject and condition. This shows
that the true prior (red line) was reliably learned by each subject.
To examine whether subjects can learn complex distributions, a new group of subjects were exposed to a bimodal distribution (Fig. 3a)
consisting of a mixture of two gaussians separated by 4 cm. Here,
the bayesian model predicts a nonlinear relationship between true shift
and lateral deviation, with the precise shape depending on the
uncertainty of the visual feedback. Figure 3b
shows a single subject's lateral deviation together with the fit of a
bayesian model (solid line) in which we fit two parameters: the
separation of the two gaussians and the variance of the visual
uncertainty. The nonlinear properties are reflected in the empirical
data and are consistent over the subjects (Fig. 3c) with a fitted separation of 4.8 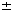 0.8 cm (mean
0.8 cm (mean 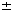 s.e.m. across subjects), close to the true value of 4 cm,
suggesting that subjects represent the bimodal prior. Taken together,
our results demonstrate that subjects implicitly use bayesian
statistics.
s.e.m. across subjects), close to the true value of 4 cm,
suggesting that subjects represent the bimodal prior. Taken together,
our results demonstrate that subjects implicitly use bayesian
statistics.
 |
Figure 3
Results for a mixture of gaussian distributions.
Full legend High resolution image and legend (29k) |
Many technically challenging problems have been addressed successfully within the bayesian framework7, 8. It has been proposed that the architecture of the nervous system is well suited for bayesian inference9-13 and that some visual illusions can be understood within the bayesian framework14. However, most models of the sensorimotor system consider a cascade of mappings from sensory inputs to the motor output15-17. These models consider input–output relationships and do not explicitly take into account the probabilistic nature of either the sensors or the task. Recent models of motor control have begun to emphasize probabilistic properties18-24. Unlike the visual system, which loses much of its plasticity once it has passed its critical period, the motor system retains much of its plasticity throughout adult life. We could therefore impose a novel prior on the subjects and measure its influence on sensorimotor processing. To show quantitatively that the system performs optimally would require a direct measure of sensory uncertainty before it is integrated with the prior. However, such a measure cannot easily be obtained as even a naive subject would integrate feedback with their natural, but unknown, prior. However, by imposing experimentally controlled priors we have shown that our results qualitatively match a bayesian integration process. A bayesian view of sensorimotor learning is consistent with neurophysiological studies showing that the brain represents the degree of uncertainty when estimating rewards25-27 and with psychophysical studies addressing the timing of movements28, 29. Although we have shown only the use of a prior in learning hand trajectories during a visuomotor displacement, we expect that such a bayesian process might be fundamental to all aspects of sensorimotor control and learning. For example, representing the distribution of dynamics of objects, such as their mass, would facilitate our interactions with them. Similarly, although the possible configurations of the human body are immense, they are not all equally likely and knowledge of their distribution could be used to refine estimates of our current state. Taking into account a priori knowledge might be key to winning a tennis match. Tennis professionals spend a great deal of time studying their opponent before playing an important match, ensuring that they start the match with correct a priori knowledge.
Methods
Experimental details Six male and four female subjects
participated in this study after giving informed consent. Subjects made
reaching movements on a table during which an Optotrak 3020 tracking system (Northern Digital)
measured the position of their right index finger. A projection–mirror
system prevented direct view of their arm and allowed us to generate a
cursor representing their finger position that could be displayed in
the plane of the movement (for details of the set-up see ref. 30).
Subjects saw a blue sphere representing the starting location, a green
sphere representing the target and a white sphere representing the
position of their finger (Fig. 1a).
Subjects were requested to point accurately to the target. When the
finger left the start position, the cursor representing the finger was
extinguished and displaced to the right by an amount that was drawn
each trial from a gaussian distribution with mean of 1 cm and
standard deviation of 0.5 cm. Midway through the movement
(10 cm), feedback of the cursor centred at the displaced finger
position was flashed for 100 ms. On each trial one of four types
of feedback ( 0,
0,  M,
M,  L,
L, 
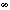 )
was displayed; the selection of the feedback was random, with the
relative frequencies of the four types being (3, 1, 1, 1) respectively.
The
)
was displayed; the selection of the feedback was random, with the
relative frequencies of the four types being (3, 1, 1, 1) respectively.
The  0 feedback was a small white sphere. The
0 feedback was a small white sphere. The  M feedback was 25 small translucent spheres, distributed
as a two-dimensional gaussian with a standard deviation of 1 cm,
giving a cloud-type impression. The
M feedback was 25 small translucent spheres, distributed
as a two-dimensional gaussian with a standard deviation of 1 cm,
giving a cloud-type impression. The  L feedback was analogous but had a standard deviation of 2 cm. No feedback was provided in the
L feedback was analogous but had a standard deviation of 2 cm. No feedback was provided in the 
 case. After another 10 cm of movement the trial was finished;
feedback of the final cursor location was provided only in the
case. After another 10 cm of movement the trial was finished;
feedback of the final cursor location was provided only in the  0 condition. The experiment consisted of 2,000 trials
for each subject. On post-experimental questioning, all subjects
reported being unaware of the displacement of the visual feedback. Only
the last 1,000 trials were used for analysis. Subjects were instructed
to take into account what they saw at the midpoint and to get as close
to the target as possible; we took the lateral deviation of the finger
from the target as a measure of subjects' estimate of the lateral
shift. By averaging over trials we could obtain this estimate
uncorrupted by any motor output noise, which we assumed to have mean of
zero.
0 condition. The experiment consisted of 2,000 trials
for each subject. On post-experimental questioning, all subjects
reported being unaware of the displacement of the visual feedback. Only
the last 1,000 trials were used for analysis. Subjects were instructed
to take into account what they saw at the midpoint and to get as close
to the target as possible; we took the lateral deviation of the finger
from the target as a measure of subjects' estimate of the lateral
shift. By averaging over trials we could obtain this estimate
uncorrupted by any motor output noise, which we assumed to have mean of
zero.
Bayesian estimation We wish to estimate the lateral shift xtrue of the current trial given a sensed shift xsensed (also known as the evidence) and the prior distribution of lateral shifts p(xtrue). From Bayes rule we can obtain the posterior distribution, that is the probability of each possible lateral shift taking into account both the prior and the evidence,
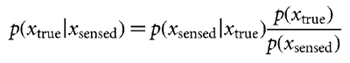

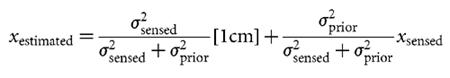
Given that we know  prior2, we can estimate the uncertainty in the feedback
prior2, we can estimate the uncertainty in the feedback  sensed by linear regression from Fig. 2a.
sensed by linear regression from Fig. 2a.
Resulting mean squared error The mean squared error (MSE) is determined by integrating the squared error over all possible sensed feedbacks and actual lateral shifts
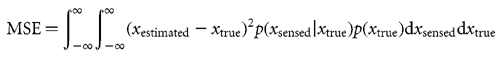
For model 1, xestimated = xsensed, and this gives MSE =  sensed2.
sensed2.
Inferring the used prior An obvious choice of xestimated is the maximum of the posterior
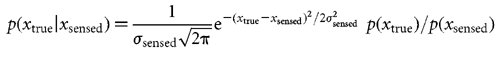
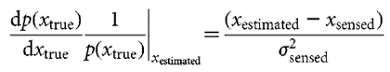
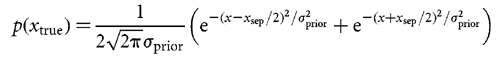
 prior = 0.5 cm. Because we expected this prior to
be more difficult to learn, each subject performed 4,000 trials split
between two consecutive days. In addition, to speed up learning,
feedback midway through the movement was always blurred (25 spheres
distributed as a two-dimensional gaussian with a standard deviation of
4 cm), and feedback at the end of the movement was provided on
every trial. Fitting the bayesian model (using the correct form of the
prior and true
prior = 0.5 cm. Because we expected this prior to
be more difficult to learn, each subject performed 4,000 trials split
between two consecutive days. In addition, to speed up learning,
feedback midway through the movement was always blurred (25 spheres
distributed as a two-dimensional gaussian with a standard deviation of
4 cm), and feedback at the end of the movement was provided on
every trial. Fitting the bayesian model (using the correct form of the
prior and true  prior) to minimize the MSE between actual and predicted
lateral deviations of the last 1,000 trials was used to infer the
subject's internal estimates of both xsep and
prior) to minimize the MSE between actual and predicted
lateral deviations of the last 1,000 trials was used to infer the
subject's internal estimates of both xsep and  sensed. Some aspects of the nonlinear relationship between lateral shift and lateral deviation (Fig. 3a)
can be understood intuitively. When the sensed shift is zero, the
actual shift is equally likely to be to the right or the left and, on
average, there should be no deviation from the target. If the sensed
shift is slightly to the right, such as at 0.25 cm, then the
actual shift is more likely to come from the right-hand gaussian than
the left, and subjects should point to the right of the target.
However, if the sensed shift is far to the right, such as at 3 cm,
then because the bulk of the prior lies to the left, subjects should
point to the left of the target.
sensed. Some aspects of the nonlinear relationship between lateral shift and lateral deviation (Fig. 3a)
can be understood intuitively. When the sensed shift is zero, the
actual shift is equally likely to be to the right or the left and, on
average, there should be no deviation from the target. If the sensed
shift is slightly to the right, such as at 0.25 cm, then the
actual shift is more likely to come from the right-hand gaussian than
the left, and subjects should point to the right of the target.
However, if the sensed shift is far to the right, such as at 3 cm,
then because the bulk of the prior lies to the left, subjects should
point to the left of the target.
Received 30 June 2003;![]() accepted 10 October 2003
accepted 10 October 2003
| 1. | van Beers, R. J., Sittig, A. C. & Gon, J. J. Integration of proprioceptive and visual position-information: An experimentally supported model. J. Neurophysiol. 81, 1355–1364 (1999) | PubMed | ISI | ChemPort | |
| 2. | Jacobs, R. A. Optimal integration of texture and motion cues to depth. Vision Res. 39, 3621–3629 (1999) | Article | PubMed | ISI | ChemPort | |
| 3. | Ernst, M. O. & Banks, M. S. Humans integrate visual and haptic information in a statistically optimal fashion. Nature 415, 429–433 (2002) | Article | PubMed | ISI | ChemPort | |
| 4. | Hillis, J. M., Ernst, M. O., Banks, M. S. & Landy, M. S. Combining sensory information: mandatory fusion within, but not between, senses. Science 298, 1627–1630 (2002) | Article | PubMed | ISI | ChemPort | |
| 5. | Cox, R. T. Probability, frequency and reasonable expectation. Am. J. Phys. 17, 1–13 (1946) |
| 6. | Bernardo, J. M. & Smith, A. F. M. Bayesian Theory (Wiley, New York, 1994) |
| 7. | Berrou, C., Glavieux, A. & Thitimajshima, P. Near Shannon limit error-correcting coding and decoding: turbo-codes. Proc. ICC'93, Geneva, Switzerland 1064–1070 (1993) |
| 8. | Simoncelli, E. P. & Adelson, E. H. Noise removal via Bayesian wavelet coring. Proc. 3rd International Conference on Image Processing, Lausanne, Switzerland, September, 379–382 (1996) |
| 9. | Olshausen, B. A. & Millman, K. J. in Advances in Neural Information Processing Systems vol. 12 (eds Solla, S. A., Leen, T. K. & Muller, K. R.) 841–847 (MIT Press, 2000) |
| 10. | Rao, R. P. N. An optimal estimation approach to visual perception and learning. Vision Res. 39, 1963–1989 (1999) | Article | PubMed | ISI | ChemPort | |
| 11. | Hinton, G. E., Dayan, P., Frey, B. J. & Neal, R. M. The 'wake–sleep' algorithm for unsupervised neural networks. Science 268, 1158–1161 (1995) | PubMed | ISI | ChemPort | |
| 12. | Sahani, M. & Dayan, P. Doubly distributional population codes: Simultaneous representation of uncertainty and multiplicity. Neural Comput. 15, 2255–2279 (2003) | Article | PubMed | ISI | |
| 13. | Yu, A. J. & Dayan, P. Acetylcholine in cortical inference. Neural Netw. 15, 719–730 (2002) | Article | PubMed | ISI | |
| 14. | Weiss, Y., Simoncelli, E. P. & Adelson, E. H. Motion illusions as optimal percepts. Nature Neurosci. 5, 598–604 (2002) | Article | PubMed | ISI | ChemPort | |
| 15. | Soechting, J. F. & Flanders, M. Errors in pointing are due to approximations in sensorimotor transformations. J. Neurophysiol. 62, 595–608 (1989) | PubMed | ISI | ChemPort | |
| 16. | Krakauer, J. W., Pine, Z. M., Ghilardi, M. F. & Ghez, C. Learning of visuomotor transformations for vectorial planning of reaching trajectories. J. Neurosci. 20, 8916–8924 (2000) | PubMed | ISI | ChemPort | |
| 17. | Lacquaniti, F. & Caminiti, R. Visuo-motor transformations for arm reaching. Eur. J. Neurosci. 10, 195–203 (1998) | Article | PubMed | ISI | ChemPort | |
| 18. | Van Beers, R. J., Baraduc, P. & Wolpert, D. M. Role of uncertainty in sensorimotor control. Phil. Trans. R. Soc. Lond. B 357, 1137–1145 (2002) | Article | ISI | |
| 19. | van Beers, R. J., Wolpert, D. M. & Haggard, P. When feeling is more important than seeing in sensorimotor adaptation. Curr. Biol. 12, 834–837 (2002) | Article | PubMed | ISI | ChemPort | |
| 20. | Harris, C. M. & Wolpert, D. M. Signal-dependent noise determines motor planning. Nature 394, 780–784 (1998) | Article | PubMed | ISI | ChemPort | |
| 21. | Todorov, E. & Jordan, M. I. Optimal feedback control as a theory of motor coordination. Nature Neurosci. 5, 1226–1235 (2002) | Article | PubMed | ISI | ChemPort | |
| 22. | Wolpert, D. M., Ghahramani, Z. & Jordan, M. I. An internal model for sensorimotor integration. Science 269, 1880–1882 (1995) | PubMed | ISI | ChemPort | |
| 23. | Vetter, P. & Wolpert, D. M. Context estimation for sensorimotor control. J. Neurophysiol. 84, 1026–1034 (2000) | PubMed | ISI | ChemPort | |
| 24. | Scheidt, R. A., Dingwell, J. B. & Mussa-Ivaldi, F. A. Learning to move amid uncertainty. J. Neurophysiol. 86, 971–985 (2001) | PubMed | ISI | ChemPort | |
| 25. | Fiorillo, C. D., Tobler, P. N. & Schultz, W. Discrete coding of reward probability and uncertainty by dopamine neurons. Science 299, 1898–1902 (2003) | Article | PubMed | ISI | ChemPort | |
| 26. | Basso, M. A. & Wurtz, R. H. Modulation of neuronal activity in superior colliculus by changes in target probability. J. Neurosci. 18, 7519–7534 (1998) | PubMed | ISI | ChemPort | |
| 27. | Platt, M. L. & Glimcher, P. W. Neural correlates of decision variables in parietal cortex. Nature 400, 233–238 (1999) | Article | PubMed | ISI | ChemPort | |
| 28. | Carpenter, R. H. & Williams, M. L. Neural computation of log likelihood in control of saccadic eye movements. Nature 377, 59–62 (1995) | Article | PubMed | ISI | ChemPort | |
| 29. | Gold, J. I. & Shadlen, M. N. The influence of behavioral context on the representation of a perceptual decision in developing oculomotor commands. J. Neurosci. 23, 632–651 (2003) | PubMed | ISI | ChemPort | |
| 30. | Goodbody, S. J. & Wolpert, D. M. Temporal and amplitude generalization in motor learning. J. Neurophysiol. 79, 1825–1838 (1998) | PubMed | ISI | ChemPort | |
Acknowledgements. We thank Z. Ghahramani for discussions, and J. Ingram for technical support. This work was supported by the Wellcome Trust, the McDonnell Foundation and the Human Frontiers Science Programme.
Competing interests statement. The authors declare that they have no competing financial interests.