#Example Graph 1
var('r1,r2,r3,r4,r5,c1,c2,c3,c4,c5');
R = [r1,r2,r3,r4,r5]; C = [c1,c2,c3,c4,c5];
G = Graph({r1:{c1:0.05,c2:0},r2:{c5:.09},r3:{c3:.04,c5:.06},r4:{c4:.02},r5:{c2:0,c4:0,c5:0}})
|
|
#Example Graph 2
var('r1,r2,c1,c2,c3');
R = [r1,r2]; C = [c1,c2,c3];
G = Graph({r1:{c1:0.05,c2:0.1},r2:{c2:.03},c3:{}})
|
|
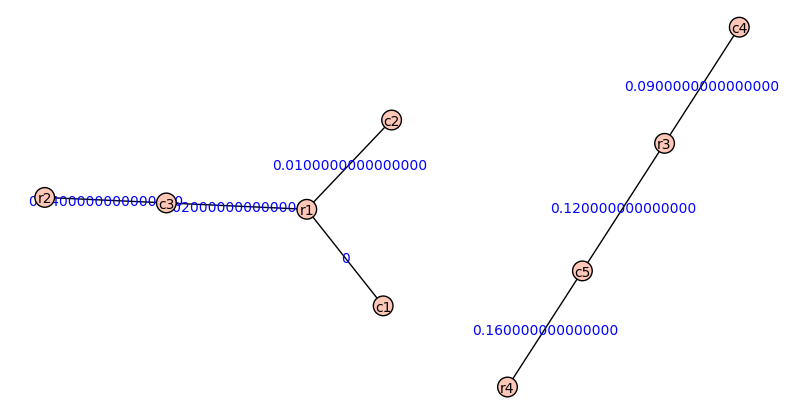
#Example Graph 3
var('r1,r2,c1,c2,c3');
R = [r1,r2,r3]; C = [c1,c2,c3,c4];
G = Graph({r1:{c1:0,c2:0.01,c3:0.02},r2:{c3:.04},r3:{c4:.09,c5:.12},r4:{c5:.16}})
|
|
G.plot(edge_labels =true)
|
|
import copy;
|
|
#Define the cycle-check function to check rank 1 conditions.
def cycle_check(G):
L = G.cycle_basis('edge');
checks = [];
for cyc in L:
p1 = prod([e[2] for e in cyc if cyc.index(e) % 2 == 0]);
p2 = prod([e[2] for e in cyc if cyc.index(e) % 2 == 1]);
checks.append(p1 == p2);
return all(checks)
|
|
#Define the rank-1 closure function.
def new_edge_value(G,e):
#Assigns the value for a new edge e = [v1,v2]
P = (G.edge_disjoint_paths(e[0],e[1]))[0];
p1 = prod([G.edge_label(P[i],P[i+1]) for i in range(len(P)-1) if i % 2 == 0]);
p2 = prod([G.edge_label(P[i],P[i+1]) for i in range(len(P)-1) if i % 2 == 1]);
return p1/p2
def r1_closure(G):
L = G.connected_components();
for H in L:
Rh = [v for v in R if v in H];
Ch = [v for v in C if v in H];
newedges = [[v,w] for v in Rh for w in Ch if not G.has_edge(v,w)];
for e in newedges:
G.add_edge((e[0],e[1],new_edge_value(G,e)))
return G
|
|
#Deals with the presence of zero edges in the graph by removing vertices whose only edges are zero (including isolated vertices). When removing vertices, try to leave more than one component while removing all zero edges.
def remove_zeros(G):
Lz = [v for v in G.vertices() if all([e[2] == 0 for e in G.edges_incident(v)])];
A = [v for v in G.vertices() if not v in Lz]
H = G.subgraph(A);
if H.is_connected():
Alist = [[v for v in G.vertices() if not v in Lz] + [w] for w in Lz]
Blist = [l for l in Alist if not G.subgraph(l).is_connected()]
if len(Blist) > 0:
C = [v for v in G.vertices() if not v in Blist[0]];
G.delete_vertices(C);
else:
G.delete_vertices(Lz)
def put_zeros_back(G,R,C):
#Returns the zeros removed at an earlier step. G is the current graph. R, C is
#original set of row and column vertices.
Rz = [v for v in R if not v in G.vertices()];
Cz = [v for v in C if not v in G.vertices()];
for v in Rz:
G.add_vertex(v);
G.add_edges([(v,c,0) for c in C if c in G.vertices()]);
for v in Cz:
G.add_vertex(v);
G.add_edges([(r,v,0) for r in R if r in G.vertices()]);
|
|
#Turns a complete bipartite graph into its corresponding matrix.
def graph_to_matrix(G,R,C):
M = matrix([[G.edge_label(R[i],C[j]) for j in range(len(C))] for i in range(len(R))]);
return M
|
|
#When G is connected, we must check: (1) all cycles consistent, and (2) that the unique rank-1 completion sums to 1. We return the unique completion, and whether it is a probability matrix.
def one_component_test(G,R,C):
if not cycle_check(G):
return "The matrix is not completable (cycles)";
else:
G2 = r1_closure(G);
put_zeros_back(G2,R,C);
M = graph_to_matrix(G2,R,C);
if sum(G2.edge_labels()) == 1:
print "The matrix is completable to: \n", M
else:
print "The matrix is not completable to a probability matrix. \n The rank-1 completion is: \n", M
|
|
#When G has two components, we must check: (1) all cycles consistent, (2) the sum of square roots of each component is at most 1. We return the two probability completions.
def two_component_test(G,R,C):
if not cycle_check(G):
print "The matrix is not completable (cycles)";
else:
G2 = r1_closure(G);
Rh = [v for v in R if v in G];
Ch = [v for v in C if v in G];
L = G2.connected_components()
if sum([sqrt(sum([e for e in H.edge_labels()])) for H in G.connected_components_subgraphs()]) > 1:
print "The matrix is not completable (half-norm)."
else:
r = [v for v in Rh if v in L[0]][0];
c = [v for v in Ch if v in L[1]][0];
var('x');
G2.add_edge((r,c,x));
G3 = r1_closure(G2);
sols = solve(sum(G3.edge_labels()) == 1,x);
put_zeros_back(G3,R,C);
N = graph_to_matrix(G3,R,C);
if len(sols) == 2:
print "The matrix is completable to: \n", N.substitute(x = sols[0].rhs()), "\n and:\n", N.substitute(x=sols[1].rhs())
else:
print "The matrix is completable to: \n", N.substitute(x = sols[0].rhs())
|
|
#When G has more components, we must check: (1) all cycles consistent, (2) the sum of square roots of each component is at most 1. We do not compute a completion, since there are infinitely many. To optimize a particular function, see the Maple code available at math.berkeley.edu/∼zhrosen/probCompletion.html
def more_components_test(G,R,C):
if not cycle_check(G):
print "The matrix is not completable (cycles)";
else:
G2 = r1_closure(G);
Rh = [v for v in R if v in G];
Ch = [v for v in C if v in G];
L = G2.connected_components()
if sum([sqrt(sum([e for e in H.edge_labels()])) for H in G.connected_components_subgraphs()]) > 1:
print "The matrix is not completable (half-norm)."
else:
print "The matrix has infinitely many completions."
|
|
#This code will check for completability. It will return a completion in the 1 and 2 component cases.
remove_zeros(G);
if 0 in G.edge_labels():
print "The matrix is not completable (zeros)";
num_cc = len(G.connected_components());
if num_cc == 1:
one_component_test(G,R,C);
else:
if num_cc == 2:
two_component_test(G,R,C);
else:
more_components_test(G,R,C);
The matrix is completable to: [ 0.000000000000000 0.0100000000000000 0.0200000000000000 -0.0300000000000000/(2*sqrt(2) - 3)] [ 0 0.0200000000000000 0.0400000000000000 -0.0600000000000000/(2*sqrt(2) - 3)] [ 0 -3/50*sqrt(2) + 9/100 -0.120000000000000*sqrt(2) + 0.180000000000000 0.0900000000000000] and: [ 0.000000000000000 0.0100000000000000 0.0200000000000000 0.0300000000000000/(2*sqrt(2) + 3)] [ 0 0.0200000000000000 0.0400000000000000 0.0600000000000000/(2*sqrt(2) + 3)] [ 0 3/50*sqrt(2) + 9/100 0.120000000000000*sqrt(2) + 0.180000000000000 0.0900000000000000] |