In this talk, I will discuss the long time behavior of a passive scalar undergoing advection diffusion by an incompressible fluid solving the stochastic 2d Navier-Stokes equations (or number of other stochastic fluid models in 3d). Specifically I will explain a recent result that uses a positive Lyapunov exponent for the Lagrangian flow to prove almost-sure exponentially fast mixing of the scalar with a rate that is uniform in the diffusivity parameter 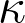. This uniform mixing implies that the scalar has an enhanced  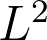dissipation effect with an optimal  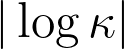time scale and that, in the forced equilibrium setting, the scalar exhibits a  power spectrum, know as Batchelor's law.